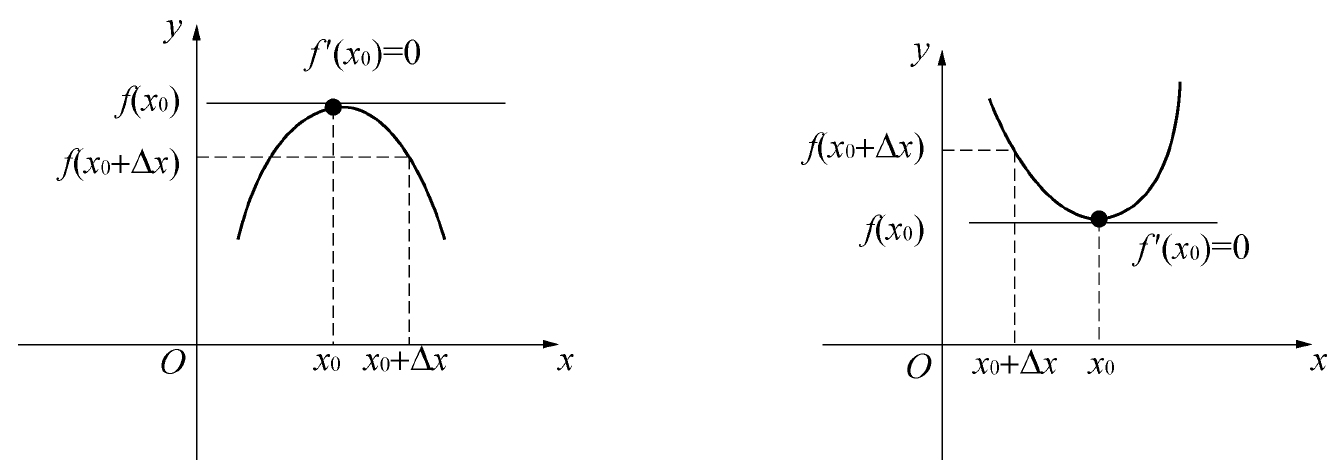高等数学(同济)
常用函数
| 函数名称 | 表达式 | 说明 |
|---|
| 幂函数 | | a 是常数 |
| 指数函数 | | a > 1单调递增;0 < a < 1单调递减 |
| 对数函数 | | a > 1单调递增;0 < a < 1单独递减;
a = e 时,自然对数
定义域 |
| | 对数函数运算性质 | ① |
| | | ② |
| | | ③ |
| | | ④ ,
它们图像关于 对称 |
| 三角函数 | | 正弦,定义域 ,值域 |
| | | 余弦,定义域 ,值域 |
| | | 正切
值域 |
| | | 余切
定义域 |
| | | 正割
|
| | | 余割
|
| 反三角函数 | | 反正弦函数,定义域,值域 |
| | | 反余弦函数,定义域,值域 |
| | | 反正切函数,定义域,值域 |
| | | 反余切函数,定义域,值域 |
| 常函数 | | 定义域,值域 |
| 绝对值函数 | | 定义域,值域 |
| 符号函数 | | 定义域,值域 |
| 取整函数 | | 不超过 x 的最大整数称为 x 的整数部分,定义域,值域整数集 |
极限
自然数
导数
| 原函数 | 导函数 | 说明 |
|---|
| | 常函数 |
| | |
| | |
| | |
| | 特别的 |
| | 特别的 |
| | |
| | |
| | |
| | |
| | |
| | |
| | |
| | |
求导
函数连续未必可导!!!,可导是函数连续的充分条件。
导数的和、差、积、商
反函数的导数等于直接函数导数的倒数.
复合函数求导
对于函数 ,有
极限与导数
特别的若
参数方程
求导
曲率
参数方程
等价无穷小
| 表达式 | 等价无穷小 | 说明 |
|---|
| | 备注1 |
| | 备注2 |
| | 备注1 |
| | 备注3 |
| | 备注4 |
| | |
| | |
备注:
麦克劳林公式
麦克劳林公式
麦克劳林公式
的麦克劳林公式
的麦克劳林公式
积分求解
极限和积分
分部积分法
常用公式
| 名称 | 详情 | |
|---|
| 立方和 | | |
| 立方差 | | |
| 二项式 | | |
| 正切,正割关系 | | |
| 平方累积和 | | |
| 不等式 | | |
| | | |
备注:
平方累积和
各项求和即可,再求解平方累积和部分结果。
定理
费马定理
设函数 在点 的某个邻域 内有定义并且在 处可导,对任意的 ,恒有 (或 ),那么 .
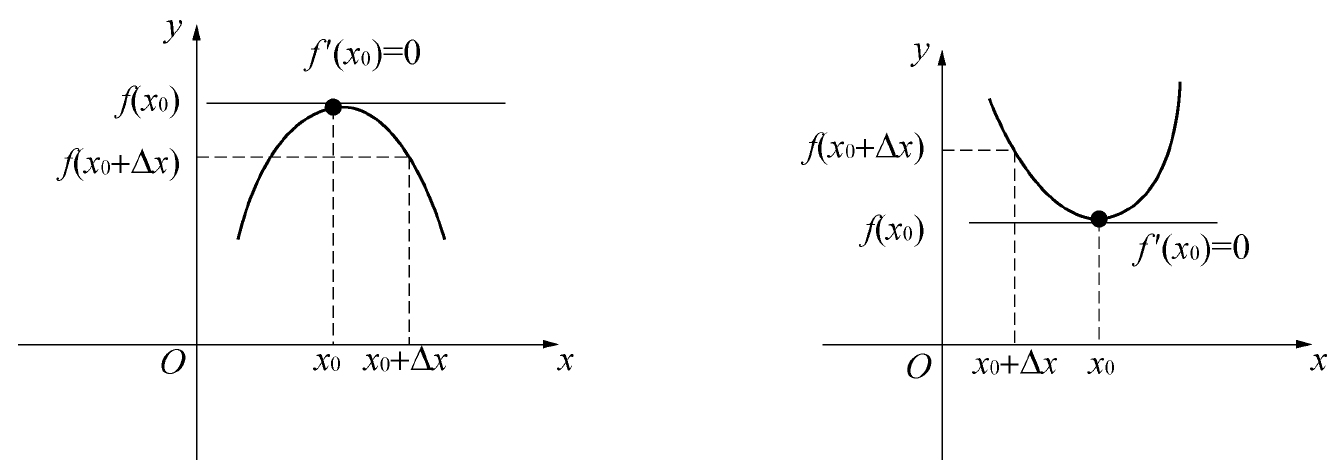
罗尔定理
函数 满足:
在闭区间 上连续
在开区间 内可导
在区间端点处的函数值相等,即
那么在 内至少有一点 ,使函数 在该点处的导数等于 0,.
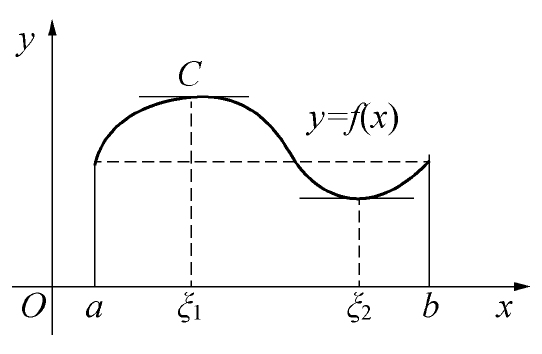
三个条件充分非必要,罗尔定理可以作为普通函数和导函数的纽带。
零点定理
若函数 在 上连续
则至少存在一点 ,使
介值定理
若函数 在 上连续
则对于 之间的任何一个数 , 在 内至少存在一点 ,使 。函数必然取的介于最小值 和最大值 之间的任何值。
拉格朗日中值定理
如果函数 满足,
在闭区间 上连续
在开区间 内可导
则至少存在一点 ,使
柯西中值定理
设函数 满足
在 上连续
在 内可导
当 时, ,
则至少存在一点 ,使得
性质
极限的保号性
单调保号:如果函数 在某区间内是单调递增或单调递减的,并且在该区间内有极限 ,则该极限 也继承该单调性。
正负保号:如果函数 在某区间内的值始终为正或为负,并且在该区间内有极限 ,则该极限 也继承该符号性质。
实例
数列极限
题目:设 ,证明 存在,并求此极限
解:证明:
因为 ,设 ,则 ,由数学归纳法可知,对任意的 ,有
因为 时,,所以 ,所以 单调递减,且 均大于 0,有下界,故 存在
令 ,对 两边同时取极限得 ,解得
可导性
在 处不可导
判断题
若 在 处可导,且 ,则 在 处一定可导
设 ,因为 ,故存在 ,当 时
,则
即 在 处可导,同理 在 处可导。
证明题
拉格朗日中值定理
若
证明:设 在区间 满足条件,又
注意:
并不正确,

将右边上移 ,函数形式并非 了


面积微元 ,扇形面积为
绕 轴的旋转体体积
绕 轴的旋转体体积
椭圆 ,绕 轴旋转体积 ,绕 轴旋转体积 ,特别的 ,即球体的体积公式为
弧长
参数方程弧长公式
星形线

微分方程
可分离变量的微分方程
齐次方程
令 ,有
应用分离变量即可。
一阶线性微分方程
当 时,下面方程为一阶齐次线性微分方程
一阶齐次线性微分方程的通解为
一阶线性微分方程通解,设为
求导
将 代入一阶线性微分方程
积分可得
代入一阶线性微分方程通解